Permutazioni e combinazioni, i vari modi in cui gli oggetti di un set possono essere selezionati, generalmente senza sostituzione, per formare sottoinsiemi. Questa selezione di sottoinsiemi viene chiamata permutazione quando l'ordine di selezione è un fattore, una combinazione quando l'ordine non è un fattore. Considerando il rapporto tra il numero di sottoinsiemi desiderati e il numero di tutti i sottoinsiemi possibili per molti giochi d'azzardo nel 17 ° secolo, i matematici francesi Blaise Pascal e Pierre de Fermat hanno dato slancio allo sviluppo della teoria combinatoria e della probabilità.
combinatoria: coefficienti binomiali
n oggetti è chiamato una permutazione di n cose prese r alla volta. Il numero di permutazioni è
I concetti e le differenze tra permutazioni e combinazioni possono essere illustrati esaminando tutti i diversi modi in cui una coppia di oggetti può essere selezionata tra cinque oggetti distinguibili, come le lettere A, B, C, D ed E. Se entrambi vengono prese in considerazione le lettere selezionate e l'ordine di selezione, quindi sono possibili i seguenti 20 risultati:

Ognuna di queste 20 diverse selezioni possibili è chiamata permutazione. In particolare, sono chiamate permutazioni di cinque oggetti presi due alla volta, e il numero di tali permutazioni possibili è indicato dal simbolo 5 P 2, leggi “5 permute 2.” In generale, se sono disponibili n oggetti da cui selezionare e si devono formare permutazioni (P) usando k degli oggetti alla volta, il numero di diverse permutazioni possibili è indicato dal simbolo n P k. Una formula per la sua valutazione è n P k = n! / (N - k)! L'espressione n! —Read “n factorial” — indica che tutti gli interi positivi consecutivi da 1 fino a compreso n devono essere moltiplicati insieme, e 0! è definito uguale a 1. Ad esempio, usando questa formula, il numero di permutazioni di cinque oggetti presi due alla volta è

(Per k = n, n P k = n! Pertanto, per 5 oggetti ci sono 5! = 120 arrangiamenti.)
Per le combinazioni, vengono selezionati k oggetti da una serie di n oggetti per produrre sottoinsiemi senza ordinamento. Contrariamente all'esempio di permutazione precedente con la combinazione corrispondente, i sottoinsiemi AB e BA non sono più selezioni distinte; eliminando tali casi rimangono solo 10 diversi sottoinsiemi possibili: AB, AC, AD, AE, BC, BD, BE, CD, CE e DE.
Il numero di tali sottoinsiemi è indicato da n C k, leggi "n scegli k". Per le combinazioni, poiché k oggetti hanno k! arrangiamenti, ci sono k! permutazioni indistinguibili per ogni scelta di k oggetti; quindi dividendo la formula di permutazione per k! produce la seguente formula di combinazione:
Questo è lo stesso del coefficiente binomiale (n, k) (vedi teorema binomiale). Ad esempio, il numero di combinazioni di cinque oggetti presi due alla volta è
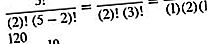
Le formule per n P k e n C k sono chiamate formule di conteggio poiché possono essere utilizzate per contare il numero di possibili permutazioni o combinazioni in una data situazione senza doverle elencare tutte.