Equazione differenziale, una dichiarazione matematica contenente uno o più derivati, ovvero termini che rappresentano i tassi di variazione di quantità in continua variazione. Le equazioni differenziali sono molto comuni nella scienza e nell'ingegneria, così come in molti altri campi di studio quantitativo, perché ciò che può essere osservato e misurato direttamente per i sistemi sottoposti a cambiamenti sono i loro tassi di cambiamento. La soluzione di un'equazione differenziale è, in generale, un'equazione che esprime la dipendenza funzionale di una variabile da una o più altre; di solito contiene termini costanti che non sono presenti nell'equazione differenziale originale. Un altro modo di dire questo è che la soluzione di un'equazione differenziale produce una funzione che può essere usata per prevedere il comportamento del sistema originale, almeno entro certi vincoli.

analisi: Newton ed equazioni differenziali
l'applicazione dell'analisi sono equazioni differenziali, che mettono in relazione i tassi di variazione di varie quantità con i loro valori attuali,
Le equazioni differenziali sono classificate in diverse grandi categorie e queste sono a loro volta ulteriormente suddivise in molte sottocategorie. Le categorie più importanti sono le equazioni differenziali ordinarie e le equazioni differenziali parziali. Quando la funzione coinvolta nell'equazione dipende solo da una singola variabile, i suoi derivati sono derivati ordinari e l'equazione differenziale viene classificata come un'equazione differenziale ordinaria. D'altra parte, se la funzione dipende da più variabili indipendenti, in modo che i suoi derivati siano derivati parziali, l'equazione differenziale viene classificata come equazione differenziale parziale. I seguenti sono esempi di equazioni differenziali ordinarie:
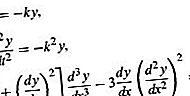
In questi, y sta per la funzione e t o x è la variabile indipendente. I simboli k e m sono usati qui per indicare costanti specifiche.
Qualunque sia il tipo, si dice che un'equazione differenziale sia dell'ennesimo ordine se coinvolge una derivata dell'ennesimo ordine ma nessuna derivata di un ordine superiore a questa. L'equazione è un esempio di un'equazione differenziale parziale del secondo ordine. Le teorie delle equazioni differenziali ordinarie e parziali sono nettamente diverse e per questo motivo le due categorie sono trattate separatamente.
Invece di una singola equazione differenziale, l'oggetto di studio può essere un sistema simultaneo di tali equazioni. La formulazione delle leggi della dinamica porta spesso a tali sistemi. In molti casi, una singola equazione differenziale dell'n-esimo ordine è vantaggiosamente sostituibile da un sistema di n equazioni simultanee, ognuna delle quali è del primo ordine, in modo che possano essere applicate tecniche dell'algebra lineare.
Un'equazione differenziale ordinaria in cui, ad esempio, la funzione e la variabile indipendente sono indicate da y e x è in effetti un sommario implicito delle caratteristiche essenziali di y in funzione di x. Queste caratteristiche sarebbero presumibilmente più accessibili all'analisi se si potesse produrre una formula esplicita per y. Tale formula, o almeno un'equazione in xey (che non implica derivati) deducibile dall'equazione differenziale, è chiamata soluzione dell'equazione differenziale. Il processo di dedurre una soluzione dall'equazione dalle applicazioni di algebra e calcolo si chiama risolvere o integrare l'equazione. Va notato, tuttavia, che le equazioni differenziali che possono essere esplicitamente risolte si formano ma una piccola minoranza. Pertanto, la maggior parte delle funzioni deve essere studiata con metodi indiretti. Anche la sua esistenza deve essere dimostrata quando non vi è alcuna possibilità di produrla per l'ispezione. In pratica, vengono utilizzati metodi di analisi numerica, che coinvolgono i computer, per ottenere utili soluzioni approssimative.