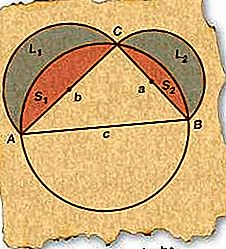
Ippocrate di Chios (fl. Circa 460 a.C.) dimostrò che le aree a forma di luna tra archi circolari, note come lune, potevano essere espresse esattamente come un'area rettilinea o quadratura. Nel seguente semplice caso, due lune sviluppate attorno ai lati di un triangolo rettangolo hanno un'area combinata uguale a quella del triangolo.
-
Partendo con il ΔABC destro, traccia un cerchio il cui diametro coincide con AB (lato c), l'ipotenusa. Poiché ogni triangolo rettangolo disegnato con un diametro del cerchio per la sua ipotenusa deve essere inscritto all'interno del cerchio, C deve trovarsi sul cerchio.
-
Disegna semicerchi con diametri AC (lato b) e BC (lato a) come in figura.
-
Etichettare le lune risultanti L 1 e L 2 e i segmenti risultanti S 1 e S 2, come indicato in figura.
-
Ora la somma delle lune (L 1 e L 2) deve essere uguale alla somma dei semicerchi (L 1 + S 1 e L 2 + S 2) che li contengono meno i due segmenti (S 1 e S 2). Pertanto, L 1 + L 2 = π / 2 (b / 2) 2 - S 1 + π / 2 (a / 2) 2 - S 2 (poiché l'area di un cerchio è π volte il quadrato del raggio).
-
La somma dei segmenti (S 1 e S 2) è uguale all'area del semicerchio in base a AB meno l'area del triangolo. Pertanto, S 1 + S 2 = π / 2 (c / 2) 2 - ΔABC.
-
Sostituendo l'espressione nella fase 5 nella fase 4 e prendendo in considerazione termini comuni, L 1 + L 2 = π / 8 (a 2 + b 2 - c 2) + ΔABC.
-
Poiché ∠ACB = 90 °, a 2 + b 2 - c 2 = 0, secondo il teorema di Pitagora. Pertanto, L 1 + L 2 = ΔABC.
Ippocrate riuscì a quadrare diversi tipi di lune, alcune su archi più grandi e meno dei semicerchi, e intimò, sebbene non avesse creduto, che il suo metodo potesse quadrare un intero cerchio. Alla fine dell'età classica, Boezio (ca. 470-524), le cui traduzioni latine di frammenti di Euclide avrebbero mantenuto la luce della geometria tremolante per mezzo millennio, menzionando che qualcuno aveva compiuto la quadratura del cerchio. Non è noto se il genio sconosciuto abbia usato le lune o qualche altro metodo, poiché per mancanza di spazio Boezio non ha dato la dimostrazione. Trasmetteva così la sfida della quadratura del cerchio insieme a frammenti di geometria apparentemente utili per eseguirla. Gli europei hanno mantenuto il compito sfortunato anche nell'Illuminismo. Alla fine, nel 1775, l'Accademia delle scienze di Parigi, stufo del compito di individuare gli errori nelle molte soluzioni presentate, si rifiutò di avere altro a che fare con gli squadratori circolari.